Cool Geometric Shapes to Draw With Reucrsion

18. Recursion¶

Recursion means "defining something in terms of itself" usually at some smaller calibration, mayhap multiple times, to accomplish your objective. For example, we might say "A man is someone whose female parent is a human being", or "a directory is a structure that holds files and (smaller) directories", or "a family tree starts with a couple who have children, each with their own family sub-trees".

Programming languages mostly back up recursion, which means that, in social club to solve a problem, functions can call themselves to solve smaller subproblems.

18.one. Drawing Fractals¶

For our purposes, a fractal is a drawing which also has cocky-similar structure, where it can be divers in terms of itself.

Let the states start past looking at the famous Koch fractal. An order 0 Koch fractal is but a directly line of a given size.

An order 1 Koch fractal is obtained similar this: instead of drawing just one line, draw instead 4 smaller segments, in the design shown here:

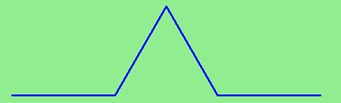
At present what would happen if nosotros repeated this Koch blueprint over again on each of the guild one segments? We'd become this order two Koch fractal:

Repeating our pattern over again gets u.s. an order 3 Koch fractal:

At present let usa think about it the other way effectually. To draw a Koch fractal of order 3, we can just describe iv order 2 Koch fractals. Simply each of these in plough needs four guild ane Koch fractals, and each of those in turn needs four order 0 fractals. Ultimately, the merely drawing that will have identify is at club 0. This is very simple to lawmaking up in Python:

i 2 3 4 5 half dozen vii 8 9 ten eleven 12 13 14 xv 16

def koch ( t , order , size ): """ Make turtle t draw a Koch fractal of 'order' and 'size'. Leave the turtle facing the aforementioned direction. """ if order == 0 : # The base case is just a straight line t . forrad ( size ) else : koch ( t , order - 1 , size / 3 ) # Become 1/3 of the manner t . left ( 60 ) koch ( t , order - 1 , size / three ) t . right ( 120 ) koch ( t , society - ane , size / 3 ) t . left ( 60 ) koch ( t , order - i , size / 3 )

The central affair that is new here is that if club is non zero, koch calls itself recursively to get its task done.

Permit's make a elementary observation and tighten up this code. Recollect that turning right by 120 is the same as turning left past -120. And then with a bit of clever rearrangement, we tin can use a loop instead of lines 10-16:

def koch ( t , guild , size ): if order == 0 : t . forrad ( size ) else : for angle in [ 60 , - 120 , 60 , 0 ]: koch ( t , order - 1 , size / 3 ) t . left ( angle )

The concluding turn is 0 degrees — and then it has no effect. Merely it has allowed united states of america to discover a pattern and reduce seven lines of code to iii, which will make things easier for our next observations.

Recursion, the high-level view

One mode to think about this is to convince yourself that the office works correctly when yous phone call it for an order 0 fractal. Then do a mental leap of faith, saying "the fairy godmother (or Python, if you tin think of Python as your fairy godmother) knows how to handle the recursive level 0 calls for me on lines 11, 13, xv, and 17, so I don't need to think virtually that particular!" All I need to focus on is how to draw an society 1 fractal if I can assume the lodge 0 one is already working.

Y'all're practicing mental brainchild — ignoring the subproblem while you solve the big problem.

If this mode of thinking works (and you lot should practice it!), so take it to the next level. Aha! now can I see that information technology will work when chosen for club 2 under the supposition that it is already working for level 1.

And, in general, if I tin assume the order due north-1 case works, tin I just solve the level n problem?

Students of mathematics who take played with proofs of consecration should meet some very strong similarities hither.

Recursion, the low-level operational view

Another mode of trying to understand recursion is to get rid of it! If we had separate functions to draw a level iii fractal, a level 2 fractal, a level 1 fractal and a level 0 fractal, we could simplify the above lawmaking, quite mechanically, to a situation where there was no longer whatsoever recursion, similar this:

one ii 3 4 5 six 7 viii 9 10 11 12 thirteen xiv 15 16 17

def koch_0 ( t , size ): t . forward ( size ) def koch_1 ( t , size ): for bending in [ sixty , - 120 , 60 , 0 ]: koch_0 ( t , size / iii ) t . left ( angle ) def koch_2 ( t , size ): for bending in [ sixty , - 120 , 60 , 0 ]: koch_1 ( t , size / iii ) t . left ( angle ) def koch_3 ( t , size ): for angle in [ 60 , - 120 , lx , 0 ]: koch_2 ( t , size / 3 ) t . left ( angle )

This trick of "unrolling" the recursion gives the states an operational view of what happens. You can trace the program into koch_3 , and from in that location, into koch_2 , and so into koch_1 , etc., all the way down the dissimilar layers of the recursion.

This might be a useful hint to build your understanding. The mental goal is, nonetheless, to exist able to do the abstraction!

eighteen.2. Recursive data structures¶

All of the Python information types we have seen can be grouped inside lists and tuples in a variety of ways. Lists and tuples tin besides be nested, providing many possibilities for organizing data. The organization of data for the purpose of making it easier to use is called a data structure.

It's election fourth dimension and nosotros are helping to compute the votes as they come in. Votes arriving from individual wards, precincts, municipalities, counties, and states are sometimes reported equally a sum total of votes and sometimes as a list of subtotals of votes. After because how best to shop the tallies, we decide to use a nested number list, which nosotros define as follows:

A nested number list is a list whose elements are either:

1. numbers
2. nested number lists

Notice that the term, nested number listing is used in its own definition. Recursive definitions like this are quite common in mathematics and information science. They provide a concise and powerful way to depict recursive data structures that are partially composed of smaller and simpler instances of themselves. The definition is non circular, since at some betoken we volition reach a listing that does not have any lists as elements.

Now suppose our job is to write a function that volition sum all of the values in a nested number list. Python has a built-in function which finds the sum of a sequence of numbers:

For our nested number listing, however, sum volition not work:

              >>>                            sum              ([              1              ,              2              ,              [              eleven              ,              13              ],              8              ])              Traceback (most recent call final):              File              "<interactive input>", line              1, in              <module>              TypeError: unsupported operand type(southward) for +:              'int' and 'list'              >>>            

The problem is that the third element of this list, [eleven, thirteen] , is itself a list, so information technology cannot just be added to 1 , ii , and 8 .

18.three. Processing recursive number lists¶

To sum all the numbers in our recursive nested number listing we need to traverse the list, visiting each of the elements within its nested structure, adding any numeric elements to our sum, and recursively repeating the summing process with any elements which are themselves sub-lists.

Thanks to recursion, the Python lawmaking needed to sum the values of a nested number list is surprisingly brusk:

def r_sum ( nested_num_list ): tot = 0 for element in nested_num_list : if type ( element ) == type ([]): tot += r_sum ( element ) else : tot += chemical element return tot

The body of r_sum consists mainly of a for loop that traverses nested_num_list . If element is a numerical value (the else co-operative), it is merely added to tot . If element is a list, so r_sum is called once more, with the element every bit an argument. The statement inside the function definition in which the function calls itself is known as the recursive telephone call.

The example above has a base of operations instance (on line 13) which does not atomic number 82 to a recursive call: the case where the chemical element is not a (sub-) list. Without a base of operations instance, you lot'll have space recursion, and your program volition not work.

Recursion is truly one of the most beautiful and elegant tools in computer science.

A slightly more complicated problem is finding the largest value in our nested number listing:

1 2 3 four v 6 7 8 9 10 11 12 xiii 14 fifteen 16 17 18 xix 20 21 22 23 24

def r_max ( nxs ): """ Notice the maximum in a recursive structure of lists within other lists. Precondition: No lists or sublists are empty. """ largest = None first_time = True for e in nxs : if type ( eastward ) == type ([]): val = r_max ( e ) else : val = e if first_time or val > largest : largest = val first_time = False render largest test ( r_max ([ 2 , 9 , [ i , 13 ], eight , 6 ]) == 13 ) test ( r_max ([ ii , [[ 100 , seven ], 90 ], [ 1 , 13 ], 8 , 6 ]) == 100 ) test ( r_max ([[[ xiii , 7 ], xc ], ii , [ 1 , 100 ], viii , 6 ]) == 100 ) test ( r_max ([ "joe" , [ "sam" , "ben" ]]) == "sam" )

Tests are included to provide examples of r_max at work.

The added twist to this problem is finding a value for initializing largest . Nosotros can't just use nxs[0] , since that could be either a element or a list. To solve this trouble (at every recursive phone call) we initialize a Boolean flag (at line eight). When we've found the value of involvement, (at line fifteen) we check to see whether this is the initializing (get-go) value for largest , or a value that could potentially change largest .

Again here we have a base case at line 13. If we don't supply a base of operations case, Python stops afterwards reaching a maximum recursion depth and returns a runtime mistake. See how this happens, by running this little script which we volition call infinite_recursion.py:

def recursion_depth ( number ): print ( "{0}, " . format ( number ), end = "" ) recursion_depth ( number + 1 ) recursion_depth ( 0 )

After watching the letters flash by, you volition exist presented with the end of a long traceback that ends with a message like the following:

RuntimeError: maximum recursion depth exceeded ...

We would certainly never desire something like this to happen to a user of one of our programs, so in the side by side chapter nosotros'll see how errors, any kinds of errors, are handled in Python.

18.4. Case study: Fibonacci numbers¶

The famous Fibonacci sequence 0, one, 1, 2, 3, 5, eight, 13, 21, 34, 55, 89, 134, ... was devised by Fibonacci (1170-1250), who used this to model the convenance of (pairs) of rabbits. If, in generation seven yous had 21 pairs in total, of which thirteen were adults, then adjacent generation the adults will all accept bred new children, and the previous children volition accept grown up to become adults. So in generation 8 you lot'll have 13+21=34, of which 21 are adults.

This model to explain rabbit convenance made the simplifying supposition that rabbits never died. Scientists frequently brand (unrealistic) simplifying assumptions and restrictions to make some headway with the problem.

If we number the terms of the sequence from 0, we can describe each term recursively as the sum of the previous two terms:

fib(0) = 0 fib(1) = 1 fib(n) = fib(n-1) + fib(n-2)  for north >= two

This translates very straight into some Python:

def fib ( n ): if due north <= 1 : render n t = fib ( n - 1 ) + fib ( n - ii ) render t

This is a especially inefficient algorithm, and nosotros'll show i fashion of fixing information technology when we learn about dictionaries:

import time t0 = fourth dimension . clock () north = 35 outcome = fib ( n ) t1 = time . clock () print ( "fib({0}) = {1}, ({2:.2f} secs)" . format ( n , result , t1 - t0 ))

Nosotros get the correct upshot, only an exploding amount of work!

fib(35) = 9227465, (x.54 secs)

18.v. Example with recursive directories and files¶

The post-obit plan lists the contents of a directory and all its subdirectories.

i 2 3 iv 5 6 7 8 nine 10 11 12 xiii xiv 15 16 17 eighteen 19 20 21 22 23

import os def get_dirlist ( path ): """ Return a sorted list of all entries in path. This returns just the names, not the full path to the names. """ dirlist = bone . listdir ( path ) dirlist . sort () return dirlist def print_files ( path , prefix = "" ): """ Impress recursive listing of contents of path """ if prefix == "" : # Observe outermost call, print a heading impress ( "Folder listing for" , path ) prefix = "| " dirlist = get_dirlist ( path ) for f in dirlist : impress ( prefix + f ) # Print the line fullname = bone . path . join ( path , f ) # Plow proper name into full pathname if os . path . isdir ( fullname ): # If a directory, recurse. print_files ( fullname , prefix + "| " )

Calling the function print_files with some folder name will produce output similar to this:

Folder list for c:\python31\Lib\site-packages\pygame\examples | __init__.py | aacircle.py | aliens.py | arraydemo.py | blend_fill.py | blit_blends.py | photographic camera.py | chimp.py | cursors.py | information | | alien1.png | | alien2.png | | alien3.png ...

18.6. An animated fractal, using PyGame¶

Hither we take a tree fractal pattern of order 8. We've labelled some of the edges, showing the depth of the recursion at which each edge was drawn.

In the tree above, the angle of deviation from the trunk is 30 degrees. Varying that angle gives other interesting shapes, for instance, with the bending at xc degrees nosotros become this:

An interesting animation occurs if we generate and draw copse very rapidly, each time varying the bending a petty. Although the Turtle module can depict copse similar this quite elegantly, nosotros could struggle for skilful frame rates. And so nosotros'll use PyGame instead, with a few embellishments and observations. (Once over again, we suggest you cut and paste this code into your Python surroundings.)

ane 2 3 four 5 vi 7 8 9 10 11 12 thirteen 14 15 16 17 xviii 19 xx 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60

import pygame , math pygame . init () # prepare the pygame module for utilise # Create a new surface and window. surface_size = 1024 main_surface = pygame . display . set_mode (( surface_size , surface_size )) my_clock = pygame . time . Clock () def draw_tree ( order , theta , sz , posn , heading , color = ( 0 , 0 , 0 ), depth = 0 ): trunk_ratio = 0.29 # How big is the trunk relative to whole tree? trunk = sz * trunk_ratio # length of trunk delta_x = body * math . cos ( heading ) delta_y = trunk * math . sin ( heading ) ( u , v ) = posn newpos = ( u + delta_x , v + delta_y ) pygame . describe . line ( main_surface , colour , posn , newpos ) if guild > 0 : # Draw another layer of subtrees # These next half-dozen lines are a simple hack to make the two major halves # of the recursion different colors. Fiddle hither to change colors # at other depths, or when depth is even, or odd, etc. if depth == 0 : color1 = ( 255 , 0 , 0 ) color2 = ( 0 , 0 , 255 ) else : color1 = color color2 = colour # brand the recursive calls to draw the two subtrees newsz = sz * ( 1 - trunk_ratio ) draw_tree ( order - 1 , theta , newsz , newpos , heading - theta , color1 , depth + one ) draw_tree ( social club - 1 , theta , newsz , newpos , heading + theta , color2 , depth + 1 ) def gameloop (): theta = 0 while True : # Handle evente from keyboard, mouse, etc. ev = pygame . result . poll () if ev . blazon == pygame . QUIT : suspension ; # Updates - change the bending theta += 0.01 # Draw everything main_surface . fill up (( 255 , 255 , 0 )) draw_tree ( 9 , theta , surface_size * 0.9 , ( surface_size // 2 , surface_size - fifty ), - math . pi / two ) pygame . display . flip () my_clock . tick ( 120 ) gameloop () pygame . quit ()

• The math library works with angles in radians rather than degrees.

• Lines 14 and 15 uses some loftier school trigonmetry. From the length of the desired line ( trunk ), and its desired bending, cos and sin help the states to summate the 10 and y distances nosotros need to move.

• Lines 22-30 are unnecessary, except if nosotros want a colorful tree.

• In the principal game loop at line 49 nosotros change the angle on every frame, and redraw the new tree.

• Line xviii shows that PyGame tin also depict lines, and enough more. Cheque out the documentation. For case, drawing a small circle at each branch point of the tree can be accomplished by adding this line straight below line 18:

  pygame . depict . circle ( main_surface , color , ( int ( posn [ 0 ]), int ( posn [ 1 ])), three )

Another interesting effect — instructive too, if you wish to reinforce the idea of different instances of the part beingness chosen at different depths of recursion — is to create a list of colors, and let each recursive depth use a different color for drawing. (Utilise the depth of the recursion to alphabetize the listing of colors.)

18.7. Glossary¶

base case

A co-operative of the conditional argument in a recursive function that does not give rise to further recursive calls.

infinite recursion

A function that calls itself recursively without ever reaching whatsoever base example. Eventually, infinite recursion causes a runtime error.

recursion

The procedure of calling a office that is already executing.

recursive call

The argument that calls an already executing role. Recursion can also exist indirect — function f can call g which calls h, and h could make a call back to f.

recursive definition

A definition which defines something in terms of itself. To be useful it must include base cases which are non recursive. In this style it differs from a circular definition. Recursive definitions often provide an elegant mode to express complex data structures, similar a directory that tin can incorporate other directories, or a menu that can contain other menus.

18.8. Exercises¶

1. Modify the Koch fractal plan so that it draws a Koch snowflake, like this:

   

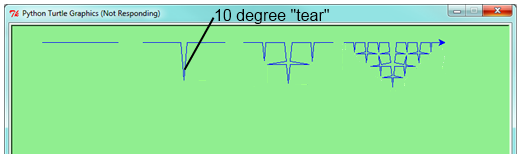
2. 1. Draw a Cesaro torn line fractal, of the order given by the user. Nosotros show four unlike lines of orders 0,1,ii,3. In this instance, the bending of the tear is 10 degrees.

      

   2. Iv lines make a foursquare. Employ the code in function a) to draw cesaro squares. Varying the angle gives interesting effects — experiment a bit, or perhaps let the user input the bending of the tear.

      
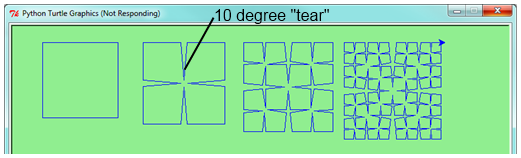
   3. (For the mathematically inclined). In the squares shown here, the higher-order drawings become a little larger. (Look at the lesser lines of each foursquare - they're non aligned.) This is because nosotros only halved the drawn part of the line for each recursive subproblem. So we've "grown" the overall square by the width of the tear(s). Can you solve the geometry trouble and so that the total size of the subproblem instance (including the tear) remains exactly the same size every bit the original?

3. A Sierpinski triangle of society 0 is an equilateral triangle. An order 1 triangle can be drawn by drawing 3 smaller triangles (shown slightly disconnected hither, just to help our agreement). College order 2 and 3 triangles are also shown. Depict Sierpinski triangles of any order input past the user.

   

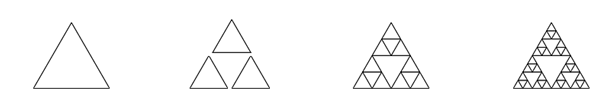
4. Adapt the to a higher place programme to change the color of its three sub-triangles at some depth of recursion. The analogy below shows 2 cases: on the left, the color is changed at depth 0 (the outmost level of recursion), on the right, at depth 2. If the user supplies a negative depth, the colour never changes. (Hint: add a new optional parameter colorChangeDepth (which defaults to -1), and brand this 1 smaller on each recursive subcall. Then, in the section of lawmaking earlier you recurse, examination whether the parameter is zero, and alter colour.)

   

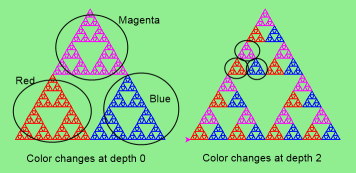
5. Write a function, recursive_min , that returns the smallest value in a nested number list. Assume in that location are no empty lists or sublists:

                     test                  (                  recursive_min                  ([                  2                  ,                  ix                  ,                  [                  1                  ,                  13                  ],                  viii                  ,                  half-dozen                  ])                  ==                  1                  )                  examination                  (                  recursive_min                  ([                  2                  ,                  [[                  100                  ,                  1                  ],                  90                  ],                  [                  ten                  ,                  xiii                  ],                  8                  ,                  6                  ])                  ==                  ane                  )                  exam                  (                  recursive_min                  ([                  2                  ,                  [[                  13                  ,                  -                  7                  ],                  xc                  ],                  [                  1                  ,                  100                  ],                  8                  ,                  6                  ])                  ==                  -                  vii                  )                  test                  (                  recursive_min                  ([[[                  -                  13                  ,                  7                  ],                  90                  ],                  two                  ,                  [                  one                  ,                  100                  ],                  8                  ,                  vi                  ])                  ==                  -                  13                  )                

6. Write a function count that returns the number of occurrences of target in a nested list:

                     test                  (                  count                  (                  two                  ,                  []),                  0                  )                  test                  (                  count                  (                  ii                  ,                  [                  2                  ,                  9                  ,                  [                  2                  ,                  1                  ,                  13                  ,                  ii                  ],                  8                  ,                  [                  2                  ,                  6                  ]])                  ==                  4                  )                  test                  (                  count                  (                  7                  ,                  [[                  9                  ,                  [                  seven                  ,                  1                  ,                  13                  ,                  2                  ],                  8                  ],                  [                  seven                  ,                  6                  ]])                  ==                  2                  )                  exam                  (                  count                  (                  15                  ,                  [[                  9                  ,                  [                  7                  ,                  i                  ,                  13                  ,                  2                  ],                  8                  ],                  [                  2                  ,                  6                  ]])                  ==                  0                  )                  test                  (                  count                  (                  5                  ,                  [[                  v                  ,                  [                  5                  ,                  [                  1                  ,                  5                  ],                  v                  ],                  5                  ],                  [                  5                  ,                  6                  ]])                  ==                  half-dozen                  )                  test                  (                  count                  (                  "a"                  ,                  [[                  "this"                  ,[                  "a"                  ,[                  "thing"                  ,                  "a"                  ],                  "a"                  ],                  "is"                  ],                  [                  "a"                  ,                  "easy"                  ]])                  ==                  iv                  )                

7. Write a function flatten that returns a simple list containing all the values in a nested list:

                     test                  (                  flatten                  ([                  2                  ,                  9                  ,[                  2                  ,                  one                  ,                  thirteen                  ,                  2                  ],                  8                  ,[                  2                  ,                  vi                  ]])                  ==                  [                  2                  ,                  9                  ,                  2                  ,                  1                  ,                  13                  ,                  two                  ,                  8                  ,                  2                  ,                  6                  ])                  test                  (                  flatten                  ([[                  9                  ,[                  7                  ,                  i                  ,                  xiii                  ,                  2                  ],                  8                  ],[                  7                  ,                  half dozen                  ]])                  ==                  [                  9                  ,                  7                  ,                  1                  ,                  13                  ,                  2                  ,                  eight                  ,                  7                  ,                  6                  ])                  test                  (                  flatten                  ([[                  9                  ,[                  7                  ,                  i                  ,                  13                  ,                  2                  ],                  eight                  ],[                  two                  ,                  6                  ]])                  ==                  [                  9                  ,                  7                  ,                  i                  ,                  13                  ,                  2                  ,                  8                  ,                  2                  ,                  6                  ])                  test                  (                  flatten                  ([[                  "this"                  ,[                  "a"                  ,[                  "thing"                  ],                  "a"                  ],                  "is"                  ],[                  "a"                  ,                  "like shooting fish in a barrel"                  ]])                  ==                  [                  "this"                  ,                  "a"                  ,                  "thing"                  ,                  "a"                  ,                  "is"                  ,                  "a"                  ,                  "easy"                  ])                  examination                  (                  flatten                  ([])                  ==                  [])                

8. Rewrite the fibonacci algorithm without using recursion. Can you notice bigger terms of the sequence? Can you discover fib(200) ?

9. Apply help to find out what sys.getrecursionlimit() and sys.setrecursionlimit(n) do. Create several experiments similar to what was done in infinite_recursion.py to exam your understanding of how these module functions work.

10. Write a program that walks a directory construction (equally in the last section of this chapter), but instead of printing filenames, it returns a list of all the full paths of files in the directory or the subdirectories. (Don't include directories in this list — just files.) For case, the output list might have elements like this:

    ["C:\Python31\Lib\site-packages\pygame\docs\ref\mask.html",  "C:\Python31\Lib\site-packages\pygame\docs\ref\midi.html",  ...  "C:\Python31\Lib\site-packages\pygame\examples\aliens.py",  ...  "C:\Python31\Lib\site-packages\pygame\examples\data\smash.wav",  ... ]

11. Write a program named litter.py that creates an empty file named trash.txt in each subdirectory of a directory tree given the root of the tree as an argument (or the electric current directory as a default). Now write a program named cleanup.py that removes all these files.

    Hint #1: Utilise the programme from the example in the final department of this affiliate as a basis for these 2 recursive programs. Considering you're going to destroy files on your disks, you better get this correct, or you lot risk losing files you care nearly. So excellent advice is that initially y'all should false the deletion of the files — just impress the full path names of each file that y'all intend to delete. Once you're happy that your logic is right, and you can come across that you're not deleting the wrong things, you can replace the print statement with the real affair.

    Hint #ii: Look in the os module for a function that removes files.

mccormicksprientake.blogspot.com

Source: https://openbookproject.net/thinkcs/python/english3e/recursion.html